Mars Exploration Rovers: Spirit and Opportunity
NASA’s Spirit and Opportunity rovers were identical twin robots that helped rewrite our understanding of the early history of Mars.
Mission Type
Objective
Destination
LandingS
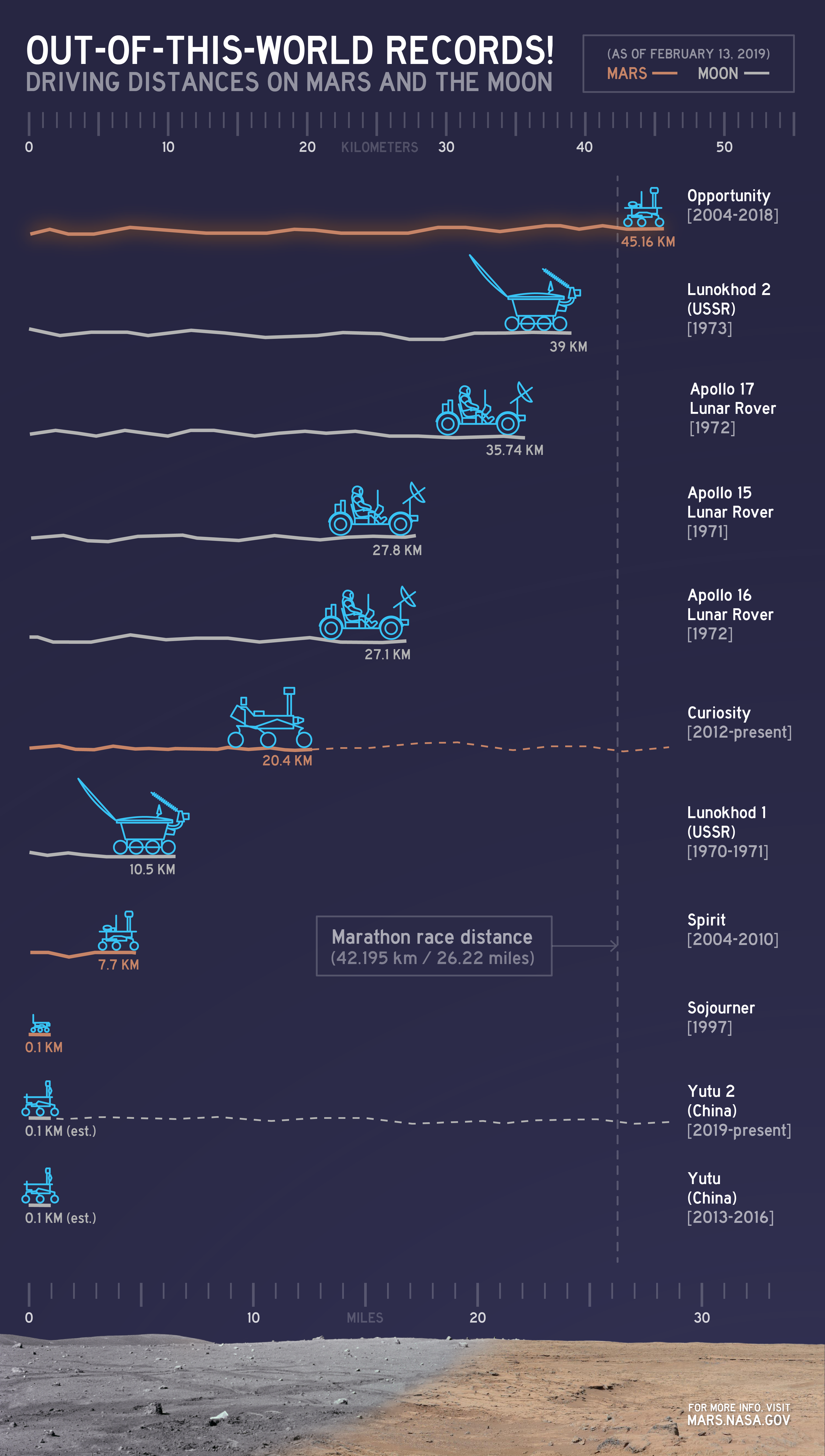
NASA’s twin rovers, Spirit and Opportunity, landed on Mars on Jan. 3 and Jan. 24, 2004 PST (Jan. 4 and Jan. 25 UTC). The rovers were planned as 90-day missions to search for geological clues regarding environmental conditions on early Mars, and assess whether those environments were conducive to life. Spirit lasted 20 times longer than its original design, concluding its mission on March 22, 2010. Opportunity worked for nearly 15 years on Mars and broke the driving record for putting the most miles on its odometer, ending its mission on Feb. 13, 2019.

Meet Spirit and Opportunity
Mars Exploration Rovers In Depth
Rover Basics
Each robotic explorer sent to the Red Planet has its own unique capabilities driven by science. Many attributes of a rover take on human-like features, such as “heads,” and “bodies.”
Objectives
New knowledge from the twin rovers uniquely contributed to meeting the four overarching goals of the Mars Exploration Program, while complementing data gathered through other Mars missions.
Science
By studying the rock record, Spirit and Opportunity confirmed that water was long standing on the surface of Mars in ancient times.
Raw Images
View raw images sent back by Spirit and Opportunity from their explorations on Mars.

Landing Sites
The rovers were targeted to land at sites on opposite sides of Mars that looked as though they were affected by liquid water in the past. Spirit landed at Gusev Crater, a possible former lake in a giant impact crater. Opportunity landed at Meridiani Planum, a place where mineral deposits suggested that Mars had a wet history.


Going the Distance
By the end of its mission, Spirit journeyed 4.8 miles (7.7 kilometers) on Mars. Opportunity holds the off-Earth roving distance record after accruing 28.06 miles (45.16 kilometers) of driving on Mars.